Knowledge Distillation of Language Models
31st October 2021
Introduction
With the rise of transformers and language models in the past few years, researchers have managed to build exceptional machine learning models for solving NLP problems and have effectively outperformed all previous methods. It's an exciting time to be working in NLP, as language models can now be repurposed via transfer learning and trained faster with GPUs compared to traditional NLP deep learning architectures. However, these models are extremely large (for example, Hugging Face’s bert-base-uncased model is made up of 110 million parameters), slow and computationally expensive, usually requiring at least one GPU to run. Thus, there is an increasing interest in building lightweight language models in order to mitigate the problems above.
"Knowledge distillation" is one of the many methods that can be used to solve this problem. For those interested in the original paper by Hugging Face, see Sanh, et al., 2020. The Hugging Face paper explains how they leverage knowledge distillation to train the DistilBERT model and results in a reduced the size of a BERT-base model by 40%, while retaining 97% of its language understanding capabilities and being 60% faster. Since DistilBERT is much lighter than the original BERT model, it can be deployed on edge device applications without the need for GPUs (check the DistilBERT model from huggingface here and start fine-tuning it on your task-specific problem).
Language Models Overview
As mentioned above, language models have dominated NLP research for the past few years due to their exceptional performance results on a variety of NLP problems. But what are language models?
An example of a popular language model is the BERT-base model from Hugging Face. These models are typically made up of multiple transformer encoder layers that have been trained to retain a deep linguistic understanding of our language. The encoder layers are made up of multi-headed attention that allows the model to understand the contexual relationship of a word with every other word in the sentence/paragraph/document. The model is given millions of documents for training (typically news and Wikipedia articles) in order to develop a good understanding of the words and grammatical structure of the english language.
This process is often called the "pre-training" process, where the model is trained by getting the model to solve a number of semi-supervised learning tasks: "masked language modelling" (i.e. fill in the missing word in the sentence) and "next sentence prediction" (i.e. what sentence comes after this sentence) on large volumes of text data. The backpropagation process during training allows the model to update its encoder layer weights in order to minimise the loss function and consequently improves its understanding of the english language.
Once "pre-training" has been succesfully performed on the model, it is said that the model has developed a general understanding of the english language (this is typically tested against GLUE benchmarks). The next step is "fine-tuning", where the model is trained against a specific NLP problem (e.g. NER, text classification, sentiment analysis etc.) so that it maximises its performance on that particular task. For a more in-depth explanation of common language model architectures, I highly recommend Alammar's blogposts.
As explained above, these models produce exceptional results when applied to unique NLP problems. It's simply a matter of getting an appropriate pre-trained model and fine-tuning it against your task-specific problem. However, as mentioned earlier, these models are very large and can often exceed the computational limits of your application. This brings us to the need for methods such as knowledge distillation and how it work.
Knowledge Distillation Overview
"Knowledge distillation" involves a larger pre-trained model (teacher) and a small (student) model that learns to mimic the behaviour of the teacher model. The goal of "knowledge distillation" is to transfer the knowledge learnt by the teacher model during its "pre-training" stage to the student model. Note that this approach is model agnostic (i.e. the student model does not have to be a transformer model, see Tang, et al. 2019).
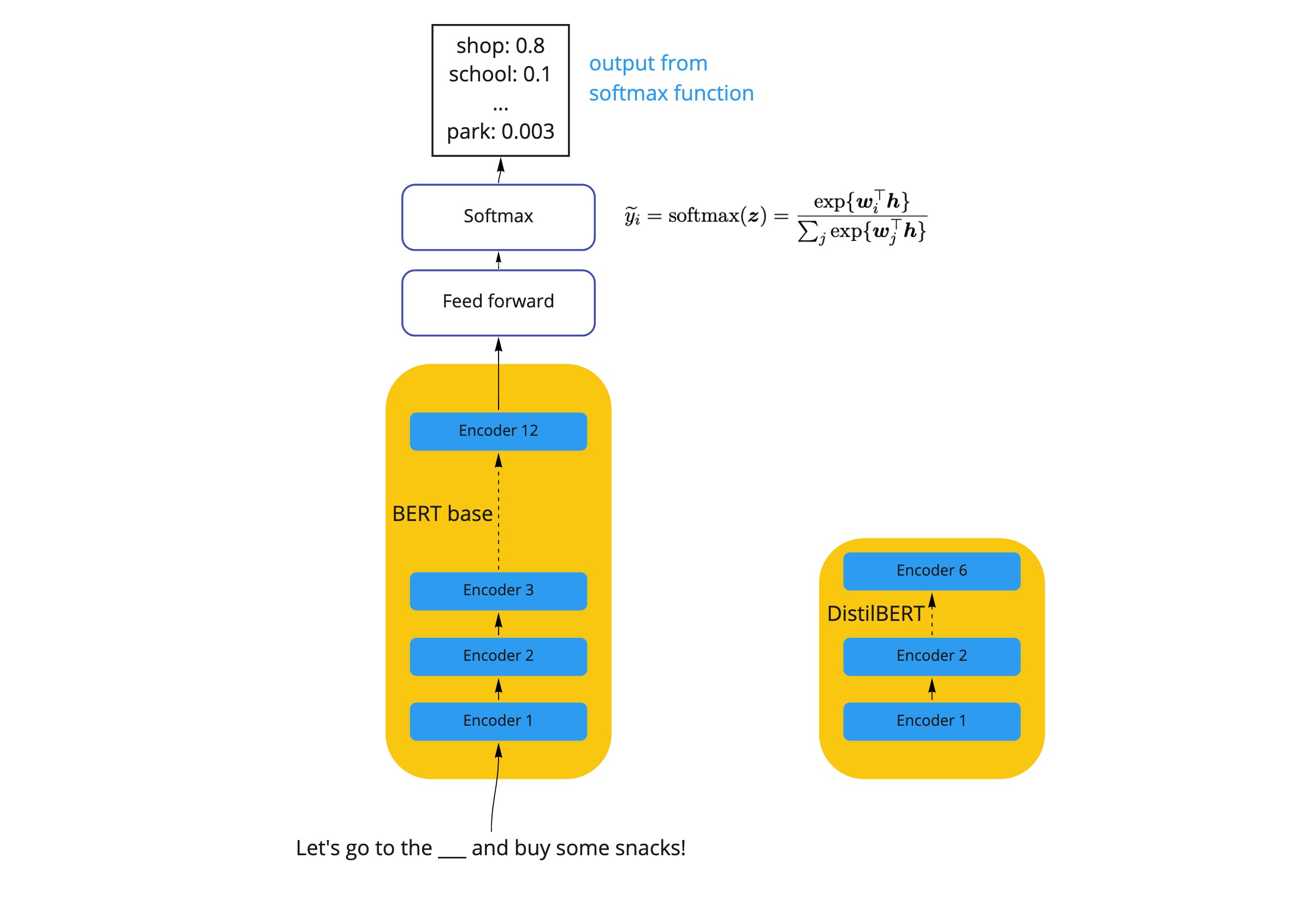
Here we will be discussing Hugging Face’s implementation of "knowledge distillation", where both the teacher and student models are transformer language models of different sizes (the teacher model being larger than the student model, of course, see the diagram below). For example, below is a diagram of a teacher and student model, where the teacher model is a BERT-base model which contains 12 encoder layers, while the student model will be the DistilBERT model which contains 6 encoder layers. The student model here is 40% smaller than the teacher model, which will naturally require less computational resources to run and also perform faster. We just need to make sure the performance results are just as good on NLP tasks as the teacher model!
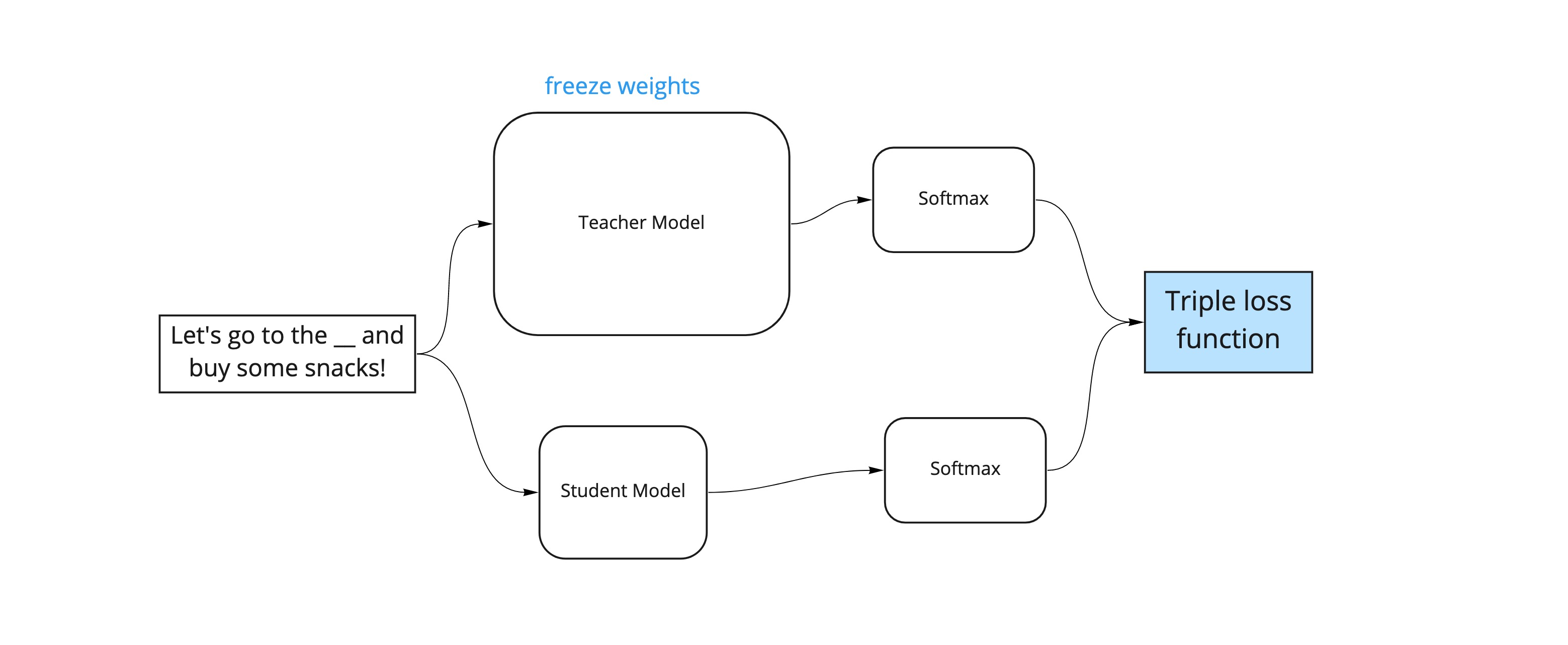
Ordinarily, when training machine learning models (e.g. on regression or classification problems), this involves minimising the loss between a model’s predictions and the training labels. However, in "knowledge distillation", instead of only learning from the training labels, the student model also learns from the teacher model.
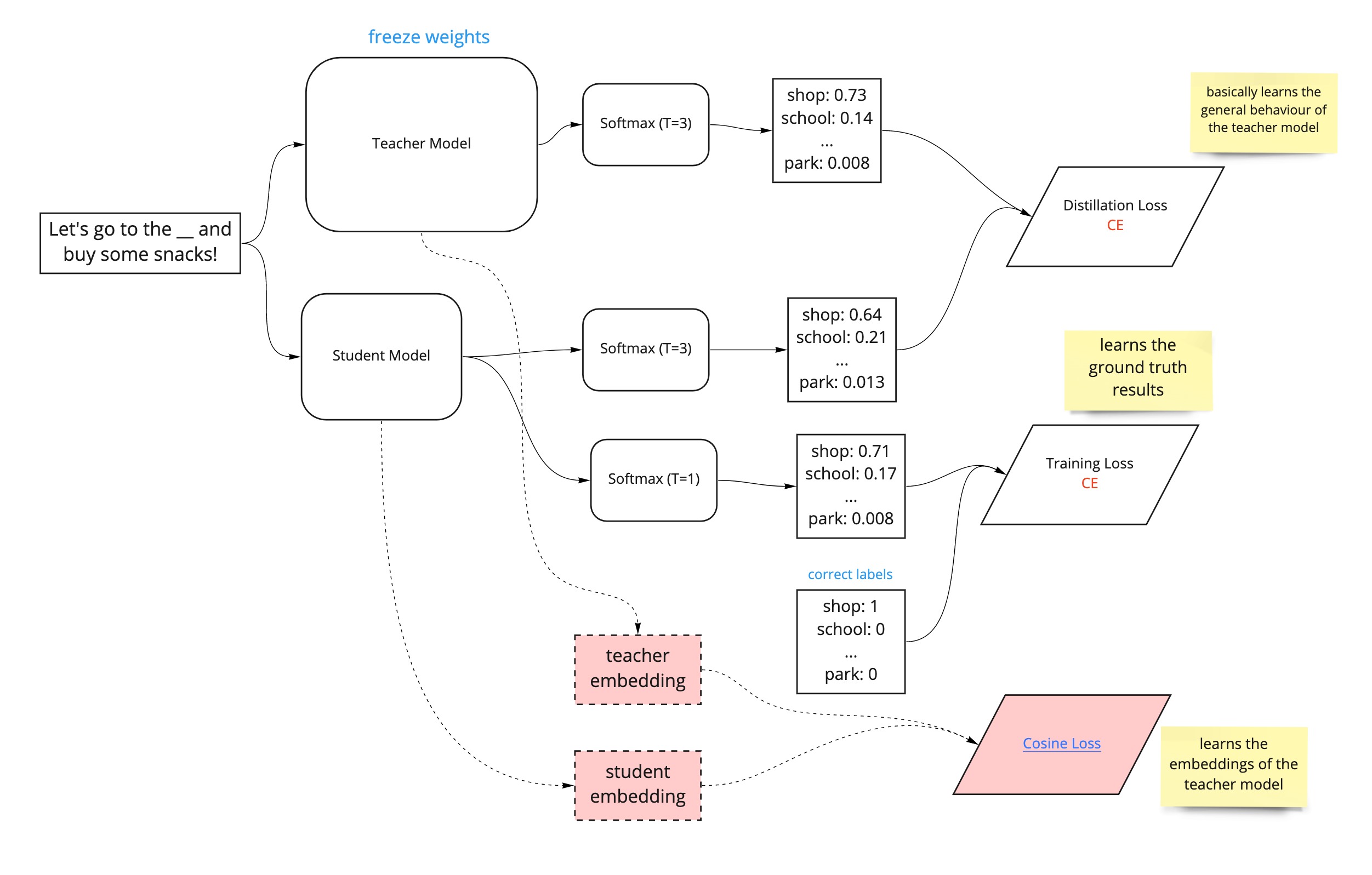
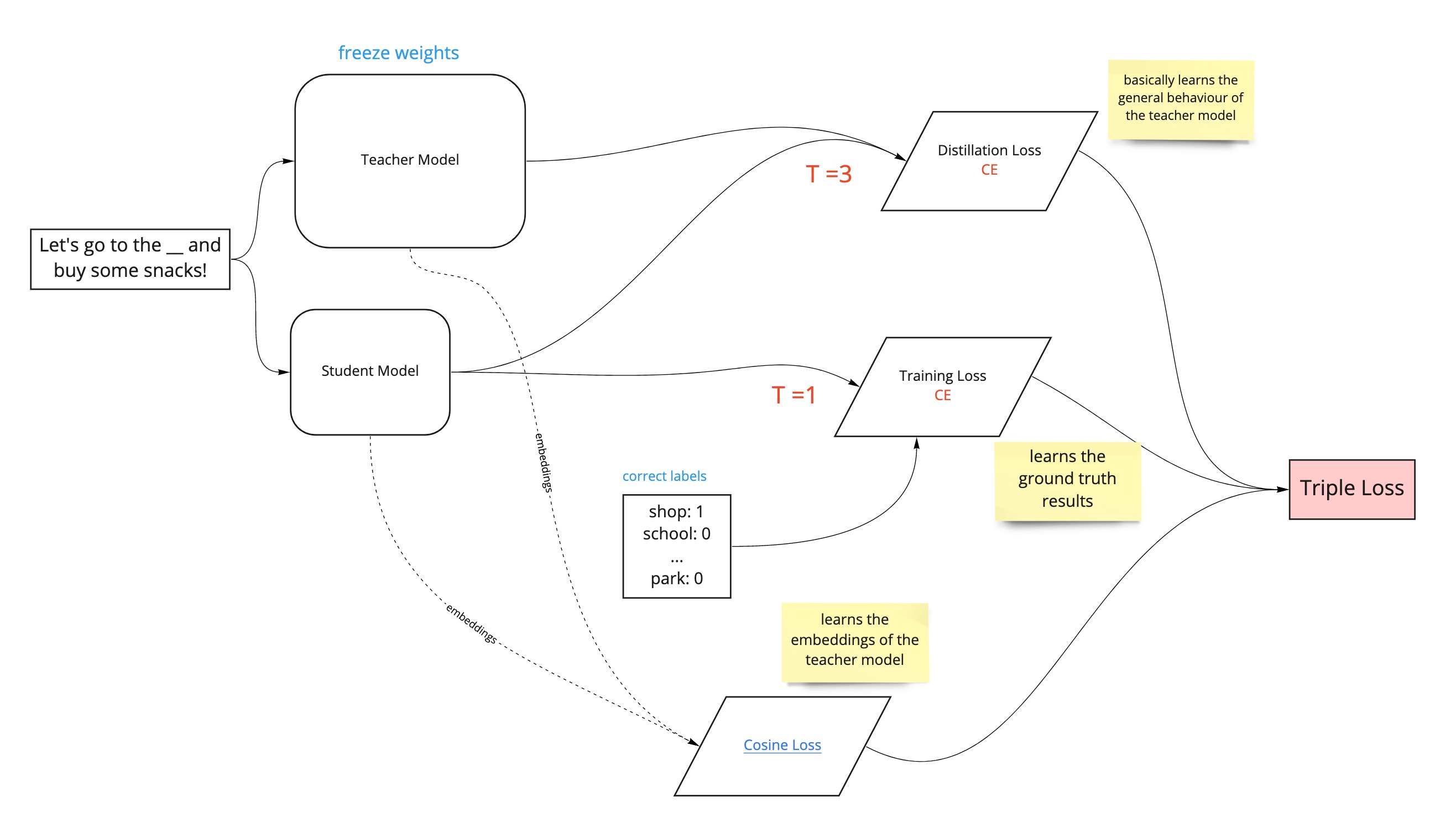
To leverage the general language understanding from the teacher model, we introduce a triple loss function that allows the student model to learn from both the training labels and teacher model (see the diagram below).
This simply involves training a deep learning network on several epochs, where each epoch will involve the back propagation process that updates the weights of the student model in order to minimise the triple loss function. Notice that the teacher model weights are frozen, so they don’t change during back propagation and effectively "freezes" the teacher model's general language understanding so that it doesn't get distorted.
Overtime, the triple loss value should become smaller after each epoch as a result of changing encoder layer weights during backpropagation, indicating that the student model is learning to output results that are more and more similar to the teacher model, and thus is learning to behave like the teacher model.
Triple Loss Function
The triple loss function is made up of a combination of the following loss functions:
- Distillation Loss
- Supervised Training Loss
- Cosine Embedding Loss
According to the DistilBERT paper, their ablation studies have shown that implementing all 3 of these loss functions produces the best results in learning the behaviour of the teacher model whilst maintaining high performance results. Below, we will go through the 3 loss functions individually in order to build a good understanding of the knowledge distillation process.
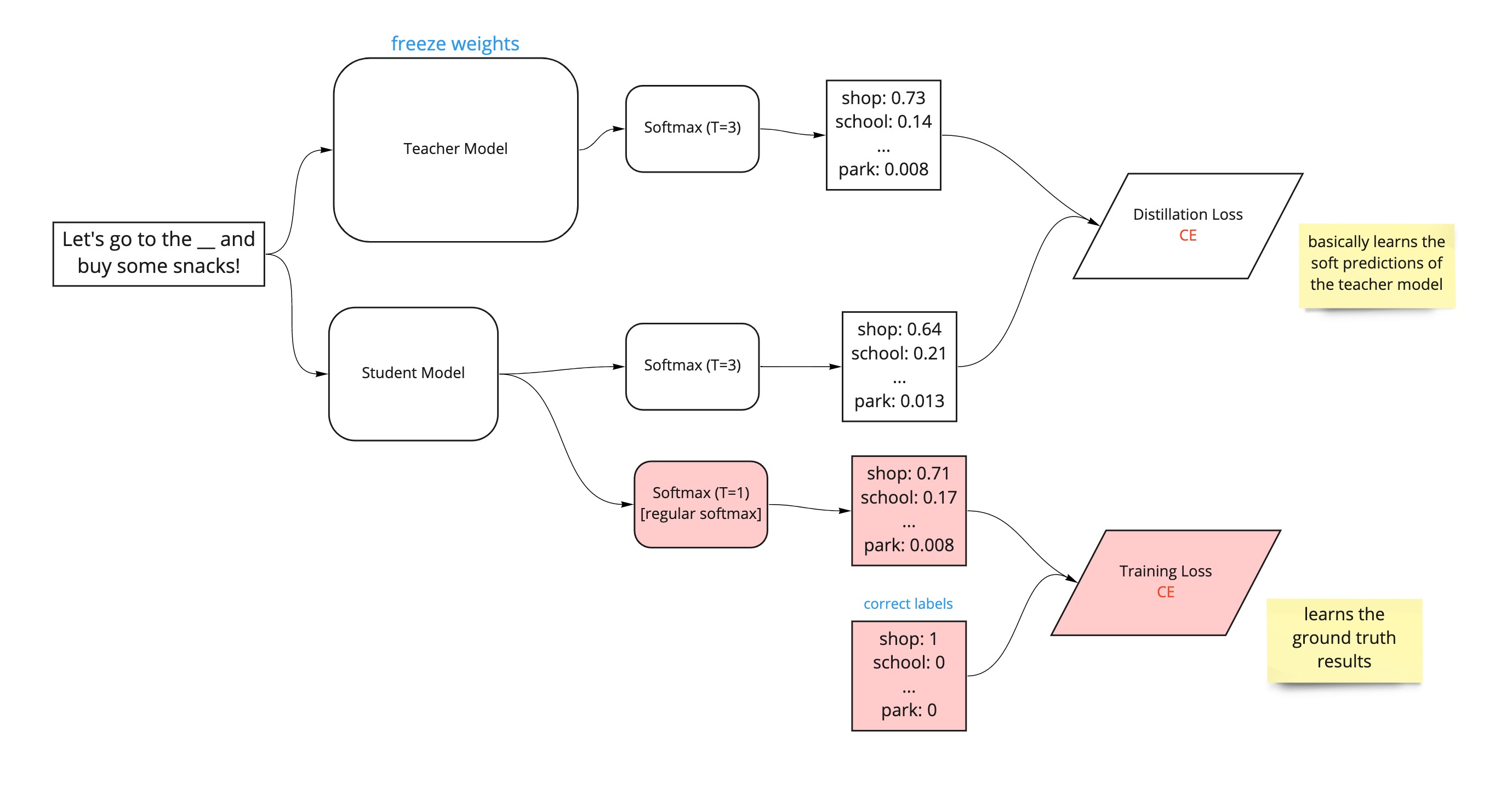
Distillation Loss
The most complicated of the 3 loss functions is the distillation loss; this involves minimising the loss against the teacher’s “soft predictions”. A teacher model performing well on a training set will produce an output distribution with high probability on the correct class and with near-zero probabilities (“soft predictions”) on the other classes. But some of these soft prediction probabilities are larger than others, and reflect, in part, the general behaviour of the model and how it will perform on new data.
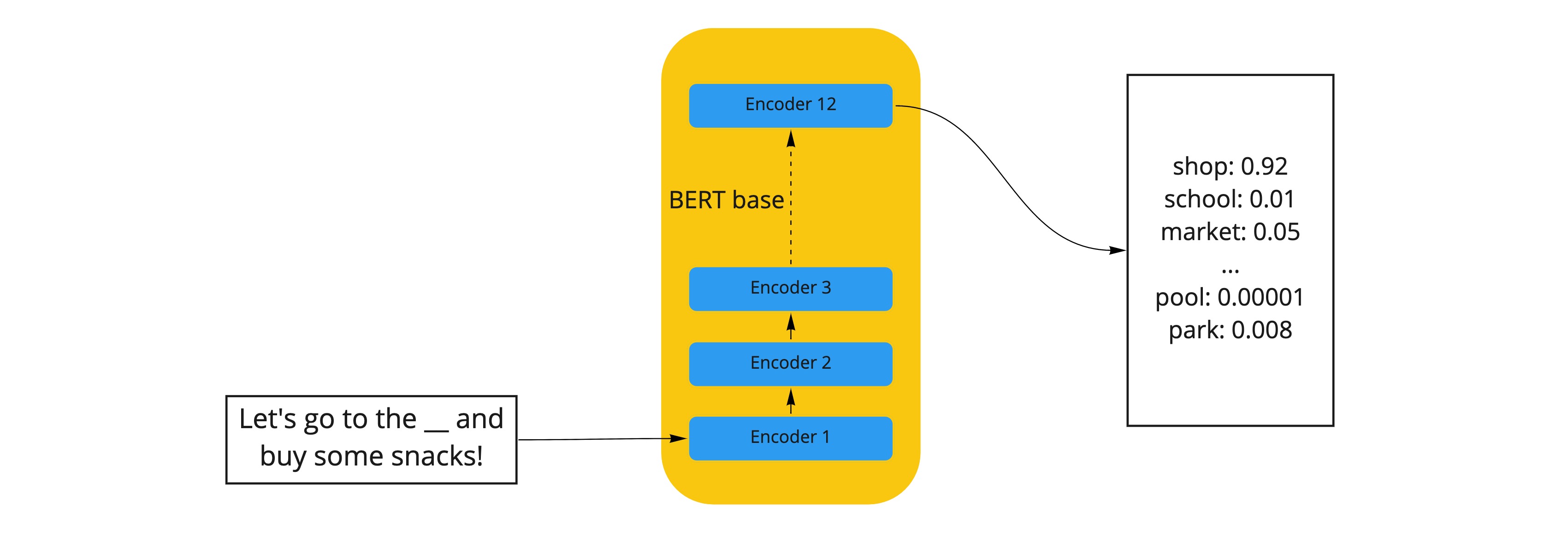
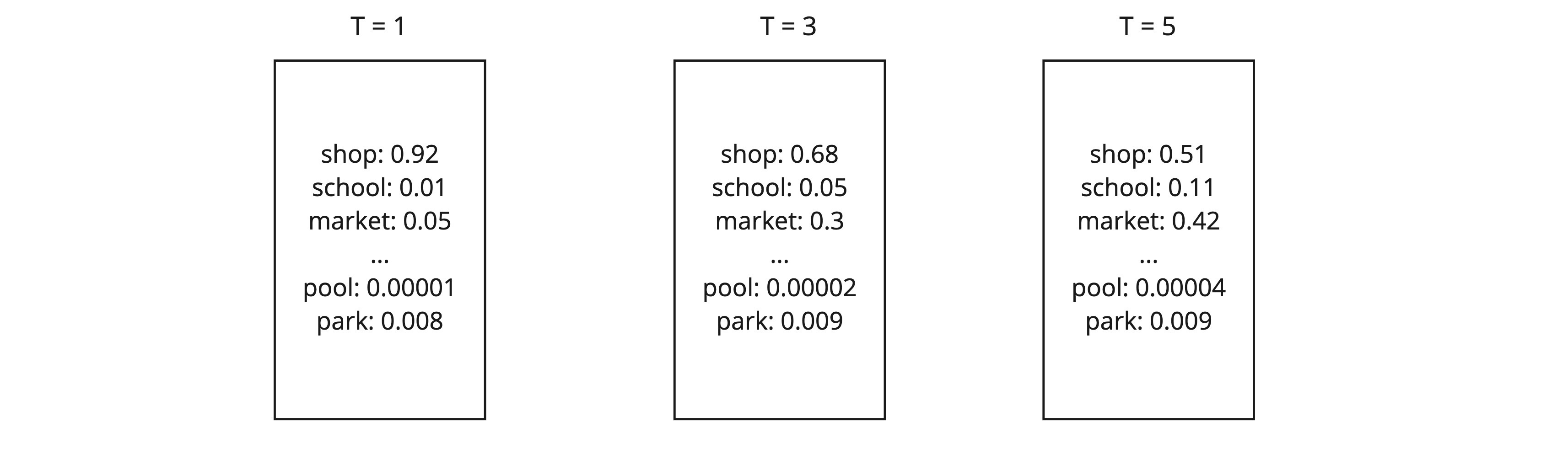
For example, in the diagram above, if we were to get the teacher model to fill in the missing word in the sentence “Let’s go to the ___ and buy some snacks!”, it produces a very high probability, 0.92, for the correct label, “shop”, and near-zero probabilities on all other labels. However, the label “market” has a slightly higher probability than, “park”, “pool”, etc. These smaller probabilities reveal some of the underlying behaviour of the teacher model, i.e., it tells us which other labels the teacher model think, other than “shop”, are closest to being the correct label. In this example, the next most likely answer is “market”.
This extra information is extremely useful, and we want to take full advantage of this! Luckily, we can leverage these “soft predictions” to teach the student model the general behaviour of the teacher model by using the Softmax temperature function as suggested by Hinton et al. 2015 (see the equation below).
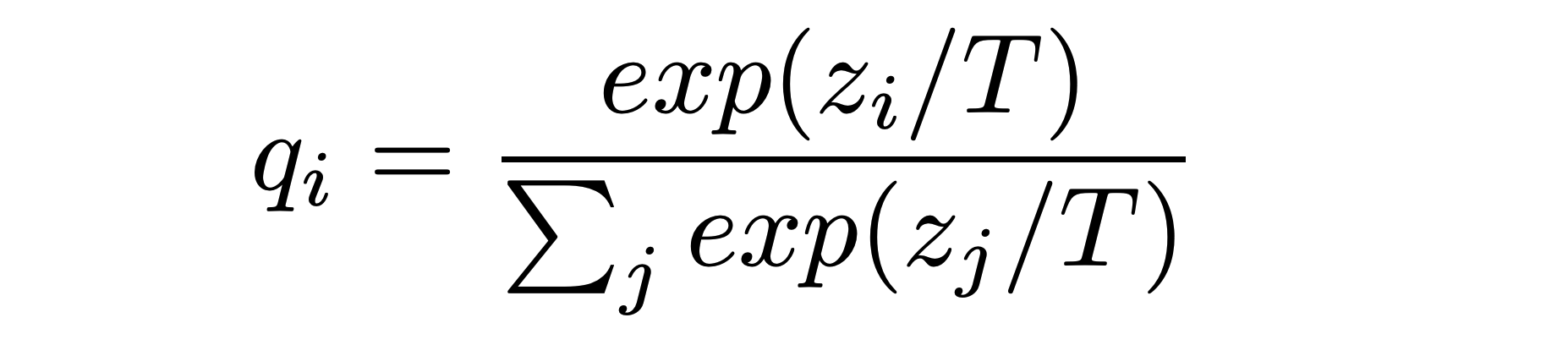
As we know, the normal SoftMax activation function is used to normalize logits from the final layer of a neural network into a probability distribution. The SoftMax temperature function does exactly the same thing, but it has an extra factor, T, also known as the temperature. T controls the smoothness of the distribution and is always set to 1 in the normal SoftMax function. Using a higher value for T produces a softer probability distribution over classes.
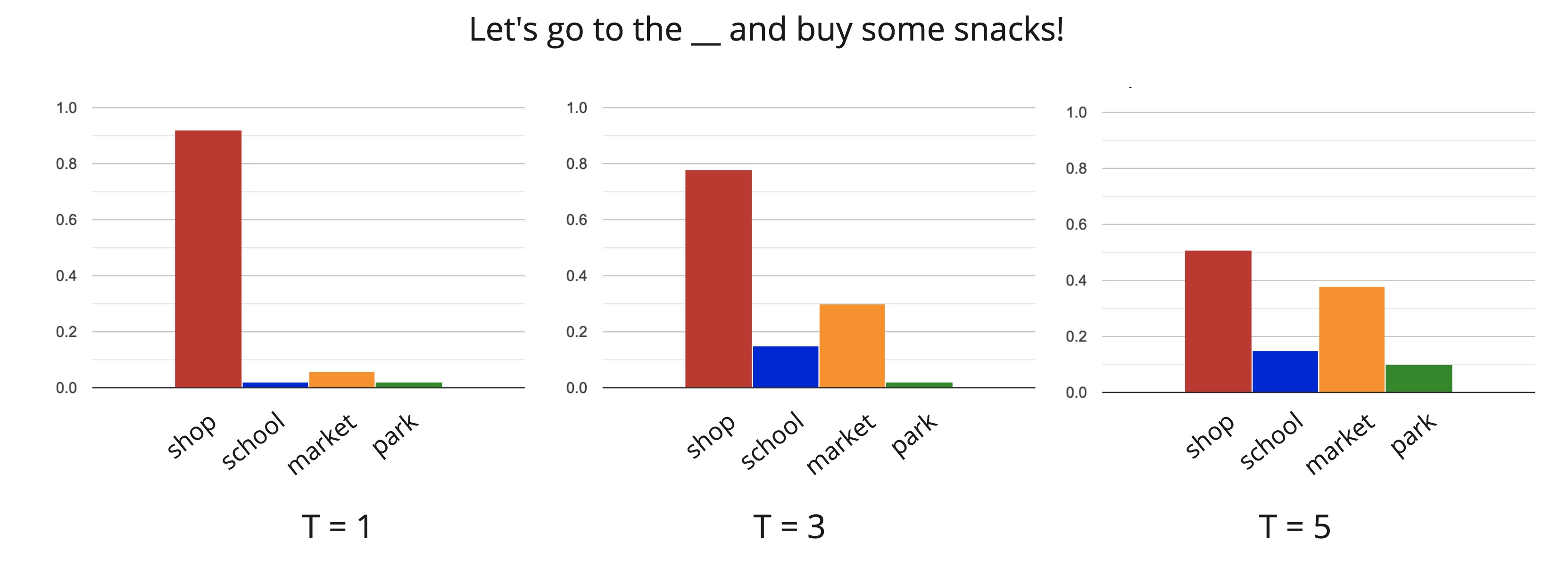
For example, as you increase T, the near-zero probabilities become slightly larger and reveals the model's “soft predictions”, i.e., what other answers the teacher model thinks could be correct. For example, see the diagram below, when T = 5, we can clearly see that the next highest probability after the correct answer “shop” is “market”, then “school”, etc.
Below is a graphical representation of how the probability distributions of the predicted answers change with respect to the temperature increasing for this particular example of filling the missing word.
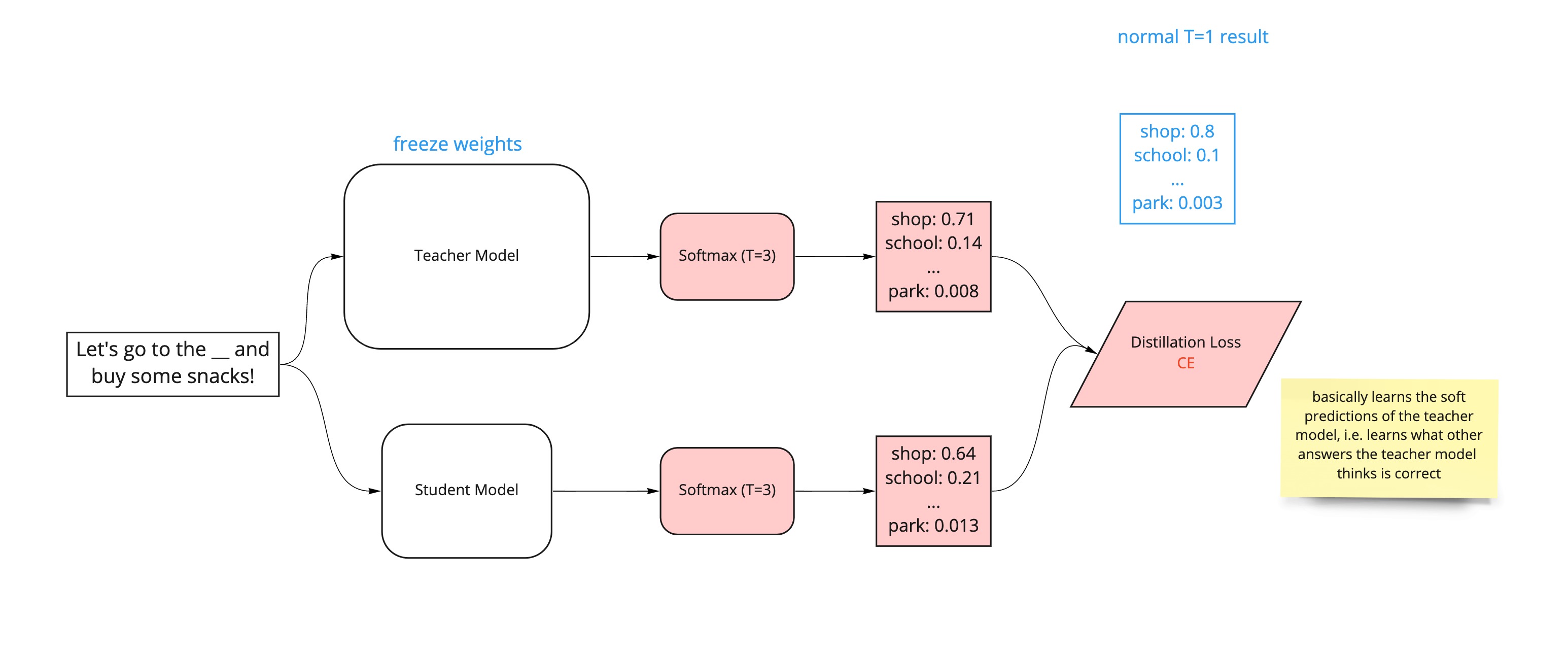
We basically want to use the SoftMax temperature function to expose the underlying "soft predictions" of the teacher model and get the student model to mimic these results. As such, we can use the SoftMax temperature function as the activation function for both the teacher and student model to normalize the outputs to a probability distribution over predicted output classes, while setting the temperature of both the teacher and student model as greater than 1 (e.g. 3).
The loss function (for example, the Kullback-Leibler divergence loss) can be used to measure the difference between the probability distributions of the student and teacher outputs from the SoftMax temperature function. The backpropagation process will alter the weights of the student model (notice we want to freeze the weights of the teacher model so we don't change its inherent behaviour and performance) in order to reduce this loss function and indirectly learn the underlying behaviour and of the teacher model (see the pink highlights in the diagram below).
Supervised Training Loss
The second loss function is the one we're most familiar with, the cross-entropy loss of the student predictions at T = 1 against the correct labels. This is identical to usual process of supervised training (minimising the loss of the model predictions against the correct labels). It simply involves computing the probability distributions with the normal SoftMax function (i.e. the SoftMax temperature function with a temperature of 1) against the ground truth (or the one-hot labels of the teacher output if correct labels are unavailable). This additional loss function will be calculated alongside the distillation loss above, and ensures that the student model is actually learning to predict the "correct" answers when T = 1 and not just the general behaviour of the teacher model (see the pink highlights in the diagram below).
Cosine Embedding Loss
The paper also mentions using a cosine-embedding loss which will help align the directions of the student and teacher hidden state vectors. Basically, a cosine similarity distance measure between the word embeddings learned by the teacher and student models. Minimizing the cosine embedding loss allows the student to learn the word embeddings of the teacher. This additional loss function will be calculated alongside the distillation loss and supervised training loss above (see the pink highlights in the diagram below).

Final architectue
So, knowledge distillation can be performed by calculating a number of loss functions that allow the student model to inherit the general knowledge and word embeddings of the teacher model and learn from the training labels. This involves minimising the triple loss function, made up of the distillation loss (which learns the general behaviour of the teacher model), supervised training loss (which learns from the training data to actually retain good performance on the task) and cosine embedding loss (which learns the word embeddings of the teacher model). This can be graphically represented by the diagram below.
Perhaps the final triple loss function can be defined as such below:
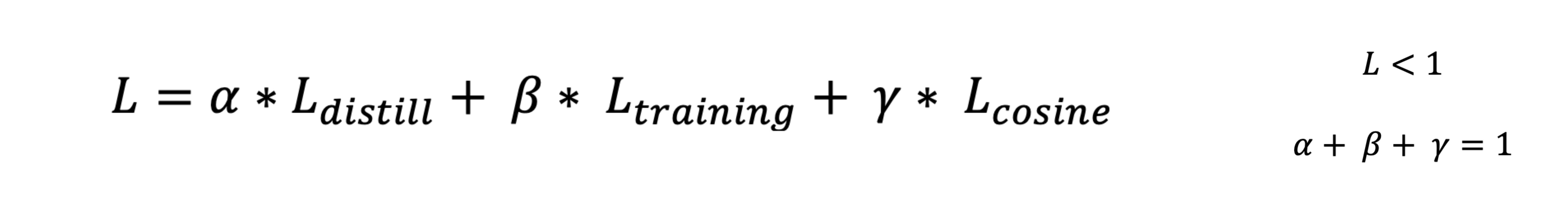
Final Comments
Knowledge distillation is an extremely interesting way to speed up BERT models without sacrificing too much performance. The DistilBERT paper states that the DistillBERT model retains almost 97% of the original BERT-base model's language undersetanding when evaluated on GLUE benchmarks. In addition to this, it is 40% smaller and 60% faster at inference.
However, note that this particular type of knowledge distillation is performed during the pre-training stage of language model training. It does not inherit, nor is it fine-tuned for any specific NLP task yet. Therefore, it functions simply as a pre-trained language model that needs to be fine-tuned on a task-specific problem to do more than just "masked language modelling".
In fact, the DistilBERT paper specifically states that it found it beneficial to use this method for general-purpose pre-training distillation rather than a task-specific distillation. If the aim is to produce a task-specific lightweight DistilBERT model, it is generally recommended to take the DistilBERT model from HuggingFace and to fine-tune this on the specific NLP task of your choice (as you would with any other BERT model).
This post should provide you with a basic understanding of knowledge distillation, acting as a foundation for understanding more advanced types of distillation methods. For example, this this TinyBERT paper by Jiao, et al., 2020 illustrates how task-specific distillation can be achieved through intermediate transformer layer distillation and therefore inherit the NER capabilities of another fine-tuned model instead of the general knowledge understanding derived from model pre-training.
Note that there are also other methods for speeding up your BERT models, such as model pruning, quantization, batching, etc. It is a very exciting area of NLP research with a lot of useful applications for companies aiming to deliver a product or service that utilises state-of-the-art language models in a lightweight fashion. It's still a relatively new field but things are moving very quickly, so be sure to watch this space.