24th April 2023
Introduction
ChatGPT’s ability to generate coherent and fluent text responses to an assortment of natural language instructions has revolutionised the field of natural language processing (NLP), and has captured the attention of the world. This type of large language model (LLM) has been trained under a new training paradigm.
Traditionally, large-scale pretraining would be performed with internet data on the language model, and then fine-tuning the model on a downstream task would result in huge performance gains for that specific task. However, when we want to build a model that generalises across hundreds of different natural language tasks, the data required for SFT is practically impossible to acquire.
Which brings us to the topic of this article, "reinforcement learning from human feedback" (RLHF) with "proximal policy optimization" (PPO). This new training paradigm moves beyond the boundaries of task-specific supervised training; allowing us to build generalised LLMs that achieve extremely impressive results on a whole range of natural language tasks.
To understand RLHF and PPO in the context of instruction fine-tuning of LLMs we need to understand the basic concepts of reinforcement learning (RL). In this post, I aim to give an intuitive overview of how RL works, proximal gradient methods, and human feedback in the context of LLM instruction fine-tuning.
This is by no means a comprehensive overview of the field of RL, for example, Q-learning, Bellman equations and other terms and concepts are beyond the scope of this post. I’ve included the bare minimum that I believe is necessary to understand RLHF, omitting mathematical details and derivations.
The papers that I have based my post on are:
- InstructGPT paper (2022): Training language models to follow instructions with human feedback
- PPO paper (2017): Proximal Policy Optimization Algorithms
InstructGPT
InstructGPT is the model that OpenAI designed to generate text responses to general instruction prompts, wherein ChatGPT builds on top of this by providing a chatbot user interface. Thus, throughout this post, I will be referring to InstructGPT and its paper, though the design and training procedure for ChatGPT-like LLMs are practically the same.
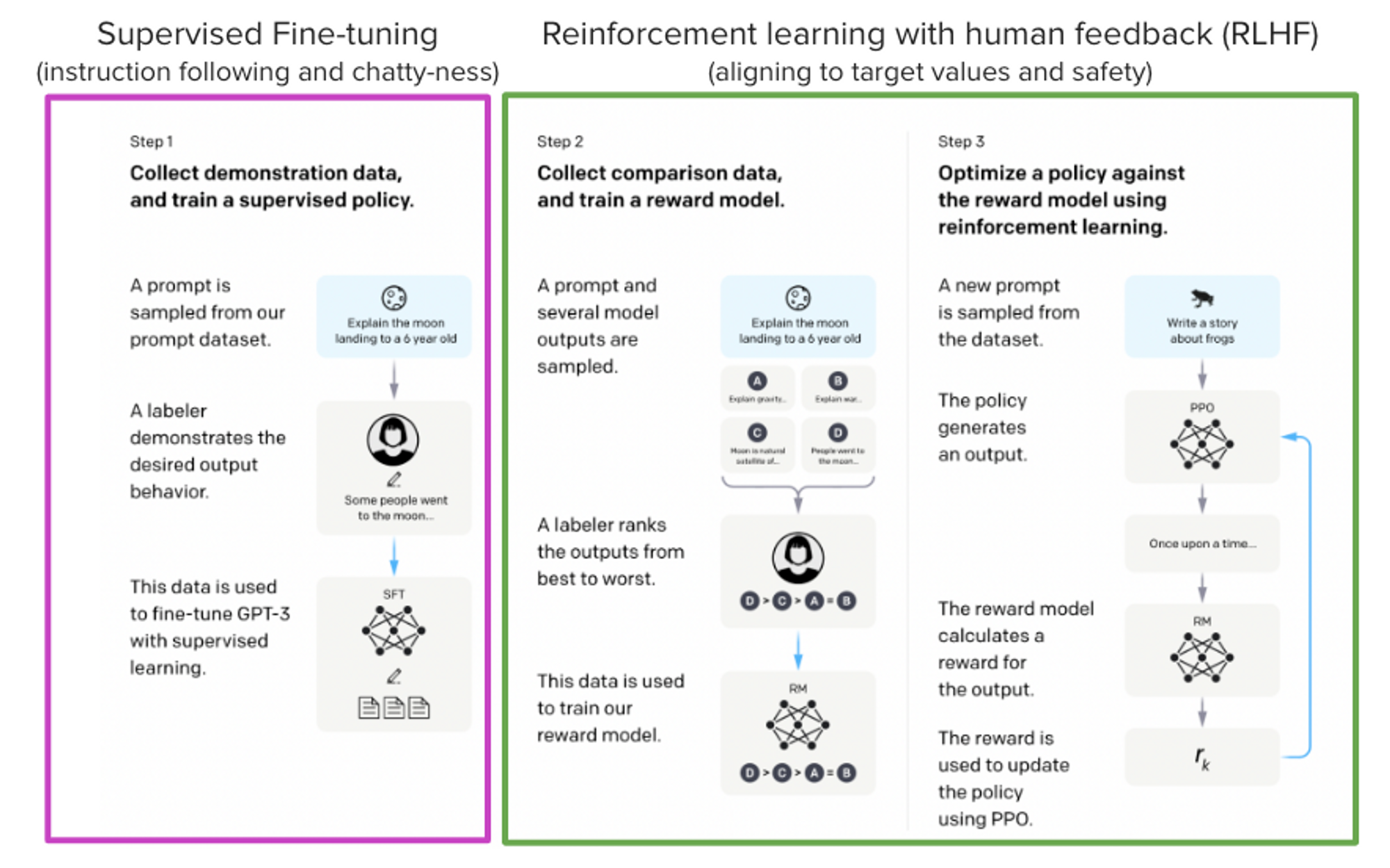
Photo credits: HuggingFace
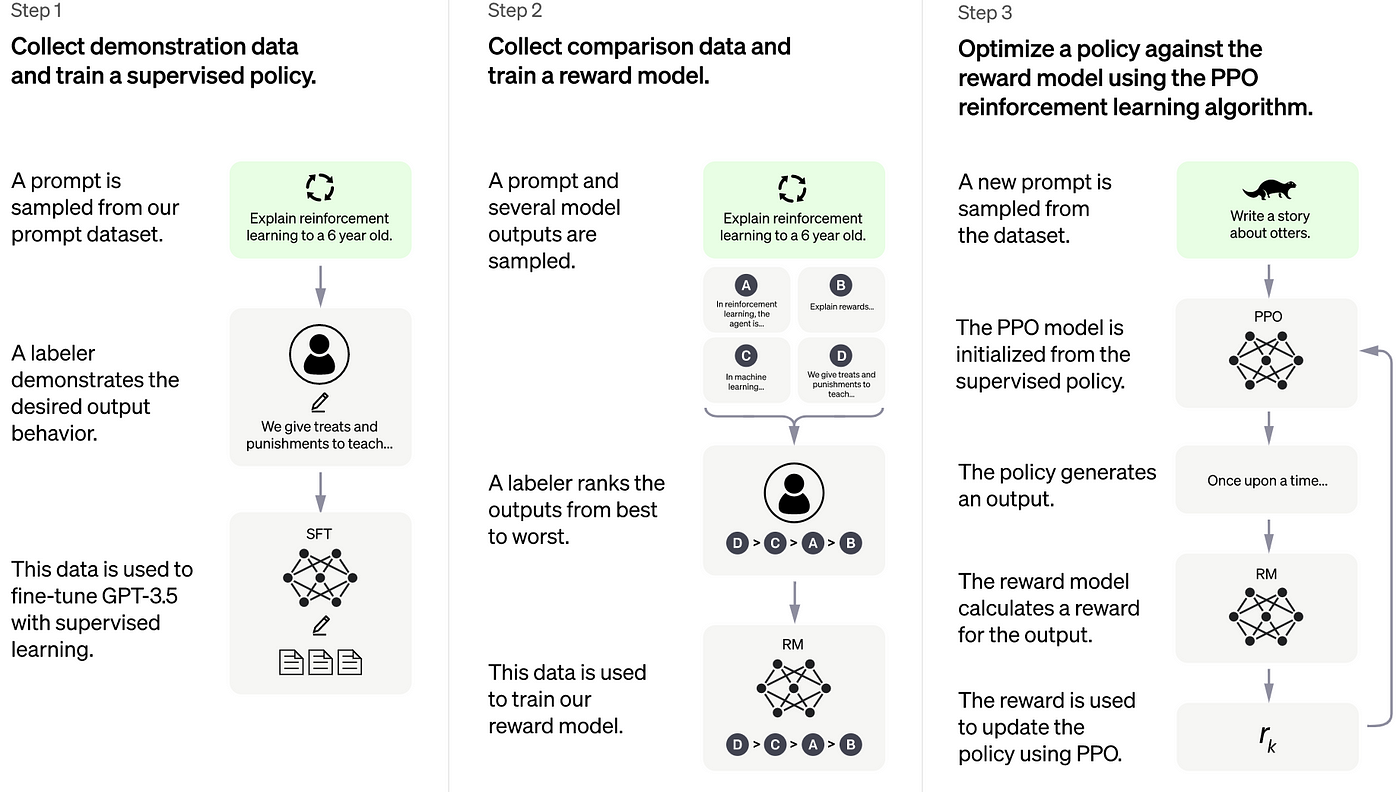
The InstructGPT paper describes the 3-step method used to train Instruct-GPT in this way:
- Taking a LLM that has already been through the pre-training stage and performs supervised fine-tuning (SFT) on a SFT dataset, consisting of a variety of instruction inputs and their ground truth answers (around 15k samples).
- Performing SFT on another LLM, to train a reward model (RM) from human feedback data, e.g. ranking scores of preferred model outputs (around 30k samples).
- Optimize the policy against the RM using Proximal Policy Optimization (PPO) with a variety of input prompts (around 31k without ground truth answers).
Step 1 is the regular SFT that we’re used to. This is a technique used to improve a LLM’s performance on a specific task or domain by fine-tuning its pre-trained weights on a smaller labelled dataset to that used during pre-training. This is an effective way to improve a model’s performance of a specific task such as text classification, sentiment analysis, and named entity recognition.
The SFT dataset contained about 13k training prompts, but it is not task specific. The SFT dataset is populated with natural language input prompts written by labellers as various instructions ranging from writing poetry, to answering questions about physics. In addition to this, each instruction prompt requires a corresponding ground truth answer from human writers.
But for training an LLM to generalise against a large variety of instruction prompts requires much more than 13k data samples. But getting human writers to come up with new prompt instructions and high-quality answers is expensive, time-consuming and extremely difficult.
Hence the need for steps 2 and 3 to accelerate the training process and overcome the need for further SFT data. But what is a reward model (RM), policy optimization, PPO? Why do we need humans in the loop? To fully understand the intuition behind all this, we need to understand the basics of reinforcement learning.
What is Reinforcement Learning (RL) ?
Reinforcement learning (RL) is a field of machine learning that aims to train agents to make good decisions in a specific environment through trial and error by receiving feedback in the form of rewards.
One of the most prominent examples of RL’s successes is the AlphaGo program developed by DeepMind around 2015: a computer program that was designed to play the board game Go, which ended up defeating the world champion Go player in a series of high-profile matches (link here https://www.deepmind.com/research/highlighted-research/alphago).
Basic definitions
In order to understand RL, we need to familiarise ourselves with the terminology used widely across RL literature:
- Agent: The entity or system that interacts with the environment and takes actions based on its current state.
- Environment: The world in which the agent operates and receives feedback in the form of rewards or penalties.
- State: The current condition or situation of the agent within the environment at a given point in time.
- Action: The decision made by the agent in response to the current state of the environment.
- Reward: The feedback received by the agent in response to its actions, which can be positive or negative. Also known as the reward signal.
- Reward Model (RM): is the model that returns the immediate reward to the agent, based on the action chosen in response to the current state (often referred to as the state-action pair). Sometimes this is called the preference model in research.
- Policy: The strategy or approach that the agent uses to select actions based on the current state of the environment.
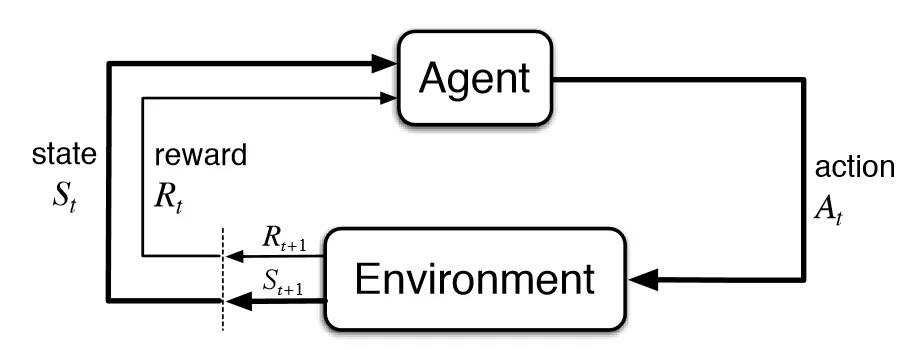
Photo credits: Medium
This figure illustrates the high-level RL pattern that typical RL systems follow. The agent is placed in an environment with a current state, which then decides on the most appropriate action to take based on its policy. Every action will cause a change in the current state, and the agent will receive a reward signal indicating whether the new state is good or bad. The goal of the agent is to learn a policy that maximises the expected cumulative reward for a given session.
In all cases of RL, our agent is usually some kind of computer system or neural network model, that is tasked with optimizing its policy (e.g., model weights) its environment to receive the highest reward possible.

RL and Super Mario Bros
To get a better grasp of how RL works, let's consider the example of an RL agent we want to teach to play the classic game of Super Mario Bros:
- Agent: The reinforcement learning agent is a computer program that learns to play the game by interacting with the environment. In the case of DRL, this would be a deep neural network that is constantly updating its weights in response to the rewards received.
- Environment: The Super Mario Bros game in itself is the environment. It consists of the game world, which includes the levels, enemies, obstacles, and power-ups.
- State: The state of the game is the current configuration of Mario’s position, the enemies, the obstacles, and the power-ups at any given moment during the game. For example, the state might include the position of Mario, the number of coins collected, and the types of enemies encountered.
- Action: In Super Mario Bros, the player can control Mario’s movements by pressing buttons on a controller. The actions that Mario can take include moving left or right, jumping, running, and shooting fireballs.
- Reward: The reward in Super Mario Bros is the points that Mario earns as he progresses through the game. For example, Mario earns points for collecting coins, defeating enemies, and completing a level. On the other hand, Mario loses points when he gets hit, or loses a life, etc.
- Policy: The policy is the strategy or approach that the agent uses to select actions against the current state. The policy might be relatively basic at first, for example: to jump every time a Koopa Trooper comes close to Mario or when a coin appears above Mario. The aim of RL is to update the policy based on the rewards received in each try.
RL and LLMs
Now that we have a basic understanding of how this works in the context of a video game, let’s consider how RL works with training LLMs to output text based on a input prompt consisting of general natural language tasks:
- Agent: The agent is the LLM itself which is being trained to generate the best responses to for a given state (prompt inputs).
- Environment: The environment is the linguistic space that the large language model has learned from a large corpus of text data.
- State: The state of the environment is the current text input to the language model. For example, if the LLM is generating a response to a text prompt, the state is the text prompt presented to it. Or if the LLM is generating the rest of a text sequence, the state is the text generated so far.
- Action: The action that a LLM can take is to generate the next word in the sequence based on the current state (e.g., generate the words based on an input prompt).
- Reward: The reward in this case is based on how well the language model is performing its task. For example, if the model is being trained to generate coherent and grammatically correct sentences, the reward function might assign a high score to sentences that are well-formed and grammatically correct, and a low score to sentences that contain errors or are nonsensical.
- Policy: The policy is defined by the model weights that were learnt during pre-training and/or SFT of the LLM. For example, given an input prompt, the LLM can generate a probability distribution of the possible next words in each text sequence based on the knowledge encoded in its model weights.
Reward Model (RM) for generating Reward Signals
To successfully train an agent via RL, we need a suitable RM that returns a reward signal based on the actions chosen by the agent. The reward is communicated to the agent, who in turn uses this information to updates its policy with the goal of maximising the expected cumulative reward for the next session.
If we return to our Super Mario Bros analogy, a simple RM (but by no means sufficient in reality) can be the scoring mechanism in the video game itself (e.g., the reward signal is the video game score for the actions taken so far in a particular level). Here, the agent’s objective is to update its current policy such that it learns the appropriate actions in each state that will lead to a higher score in the video game.
However, for LLMs, the RM itself is not so straight forward. We don’t have a scoring mechanism to tell us whether a LLM’s response to a prompt input is good or not. Designing an appropriate RM is not a trivial task as we want a RM that is informative and captures the desired behaviour of the LLM, but also easy to compute and does not lead to unintended consequences and loopholes.
Usually, in traditional supervised fine-tuning (SFT) of language models, the loss function tells us how well the model is performing, wherein the loss function calculated the discrepancy between the model’s predictions and the ground truth answers. But the problem is, we don’t have any more ground truth answers to natural language instructions anymore – nor are we looking to perform simple SFT.
So where do we find this RM that will appropriately score the text outputs of our LLM for any given instruction prompt? This is where training a RM from human feedback comes in.

Photo credits: HuggingFace
Training a RM from Human Feedback
When training an RM for RL training on LLMs, a RM dataset needs to be carefully curated by human annotators. These annotators are used to judge the overall quality of the generated text outputs from various LLMs by ranking them from the best to worst response.
One may initially think that humans should apply a scalar score directly to each piece of text to train a RM, but this is difficult to do in practice. The differing values of given by different people cause these scores to be uncalibrated and noisy. Instead, rankings are used to compare the outputs of multiple LLMs and create a much better regularized dataset.
From a practical perspective, it is also much easier to rank outputs, rather than hand-write the responses for varied text prompts. This way, OpenAI was able to collect RM dataset has 33k training prompts for the RM dataset, compared to the 13k training prompts for the SFT dataset.

Photo credits: InstructGPT paper
Another advantages of training a RM from human feedback is that the RM itself can effectively encodes the preferences of the human labellers, e.g., is this harmful, is this safe, is this funny, etc. These are very subjective values that can’t be encoded in objective loss functions – but through gathering tagged data from human labellers indicating whether the output is "harmful" or not (through human labellers with a Likert scale, see here), we can train a RM to learn how to response to the question "how harmful is this response?".
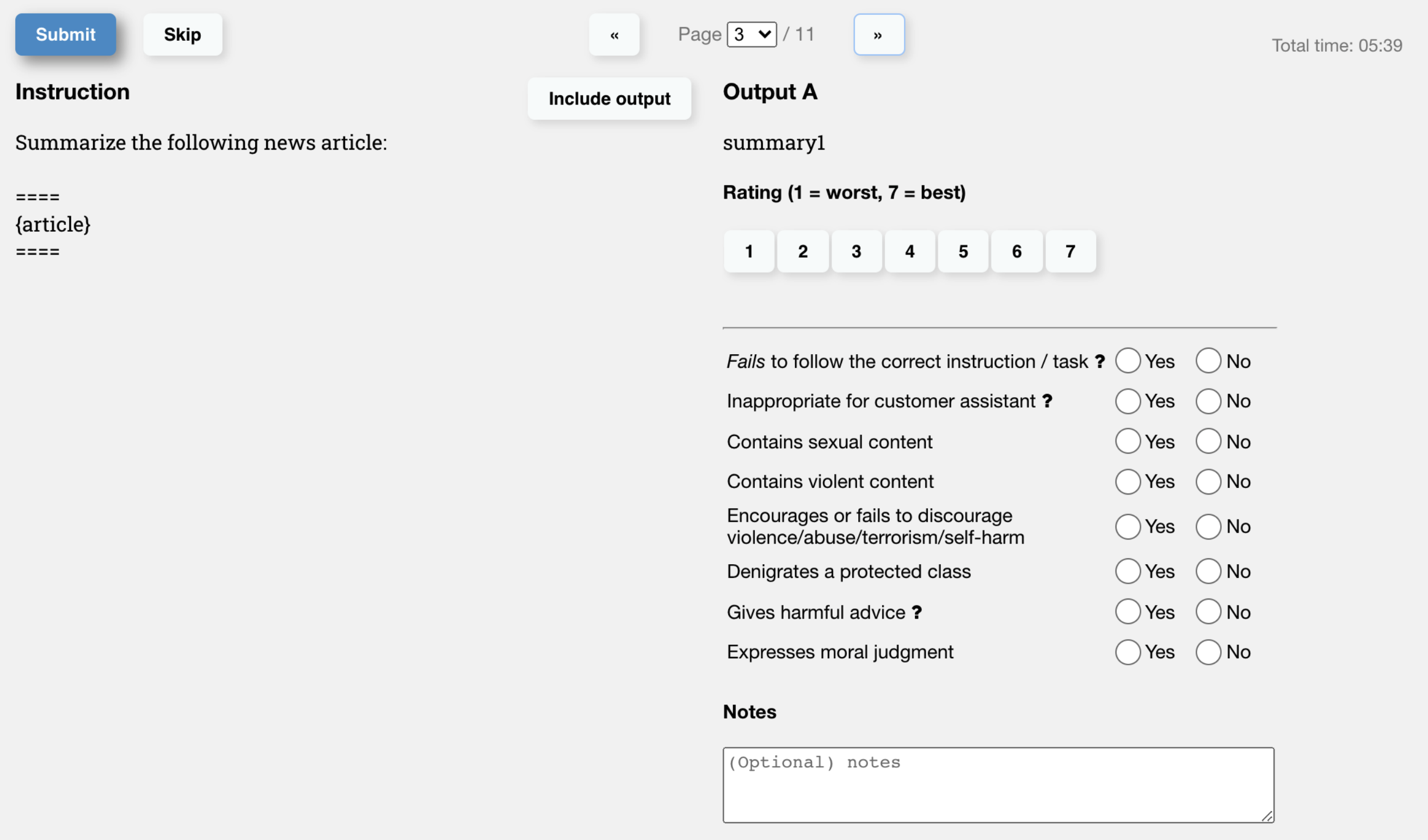
Photo credits: InstructGPT paper
This RM data is then used to perform SFT on another LLM, which effectively learns which text generated output to an instruction prompt a human labeller would prefer. Therefore, the RM learns to imitate how a human would rate an response generated to an instruction prompt. The RM will indicate whether this generated response is “good” according to the ranking preferences of human labellers - this will be presented as a reward score.
Policy Gradient Methods and the Objective Function
So, we now have a RM trained on human feedback that can signal to our LLM whether the text generated response to an input prompt is good or bad. But remember that in RL, the aim is for our LLM to learn the most optimal policy that maximises the cumulative reward for a given set of actions (the generated text response). How do we get the agent to update its policy from the reward signals?
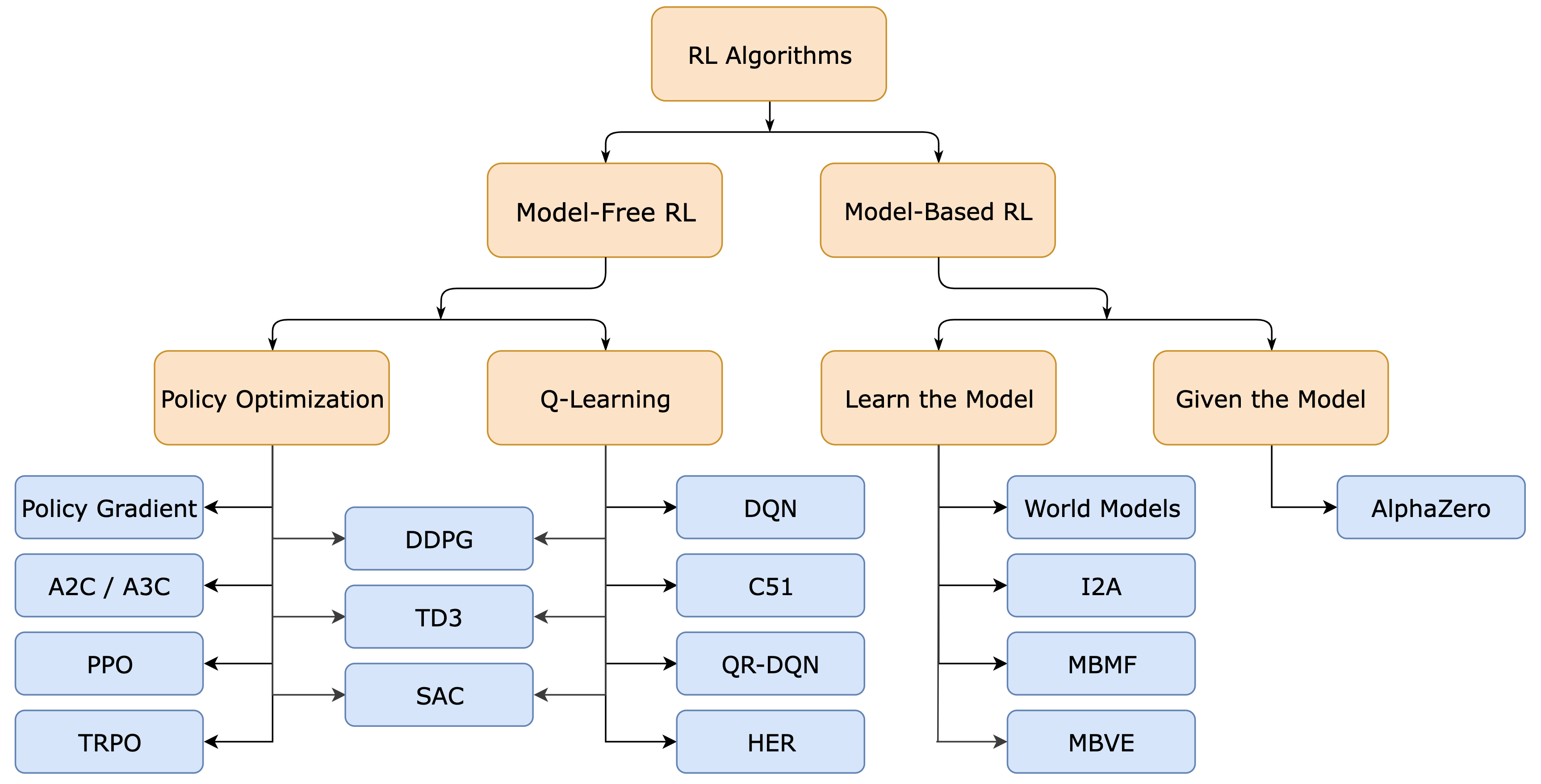
Photo credits: OpenAI - Spinning Up
In RL, there are many methods/algorithms for teaching agents to perform better, each with their own strengths and weaknesses, and their own use-cases. But for this article, we will look exclusively at a class of RL algorithms called “policy gradient methods” – and specifically that of proximal policy optimization (PPO) later. This is most relevant, as we can model the LLM training problem as a model-free RL problem – and this is also the approach used by OpenAI on InstructGPT.
Policy gradient methods aim to optimize the policy directly. For our LLMs, the policy is effectively the LLM itself, which decides what words to output based on the current state of the conversation or input prompt. Thus, the policy can be a parameterized function, wherein the parameters are the LLM weights. The optimization takes place through calculating the “policy gradients” with respect to an “objective function”. Let’s talk about these 2 new concepts.
The objective function specifies the goal that the agent is trying to achieve (i.e., maximise the expected cumulative reward for the text generated by an LLM based on the input prompts), which is often defined as a function of the policy and RM.
The main difference between the various policy gradient methods (VPG, TRPO, DPG, PPO, etc.) is how they’ve defined their objective function – each having their own advantages and disadvantages. But they all use the objective function to optimize the policy of the agent (by updating the policy parameters, i.e., the model weights).
Vanilla Policy Gradient (VPG)
Let us consider the simplest case of a policy gradient method here, the “vanilla policy gradient” (VPG), wherein the objective function can be defined as such (for the full details and derivations, please check here):

Note: the trajectory is the sequence of actions taken by the agent in response to a given state throughout the episode. For example, the word generated based on a given text sequence, then the next word generated based on the updated text sequence, and so on, until the completed text output is generated (i.e., the episode is completed).
In essence, VPG aims to maximise a very simple objective function, which is effectively the expected return from a RM for a given trajectory taken by the agent (i.e., the reward score generated from the RM for the text generated by the LLM for a given input prompt).
Here we want to use the objective function to update the policy via gradient ascent (as we want to maximise the score, unlike gradient descent when we want to minimize the score from a loss function). We can do this by optimizing the policy parameters (our model weights) by calculating the “policy gradients”.
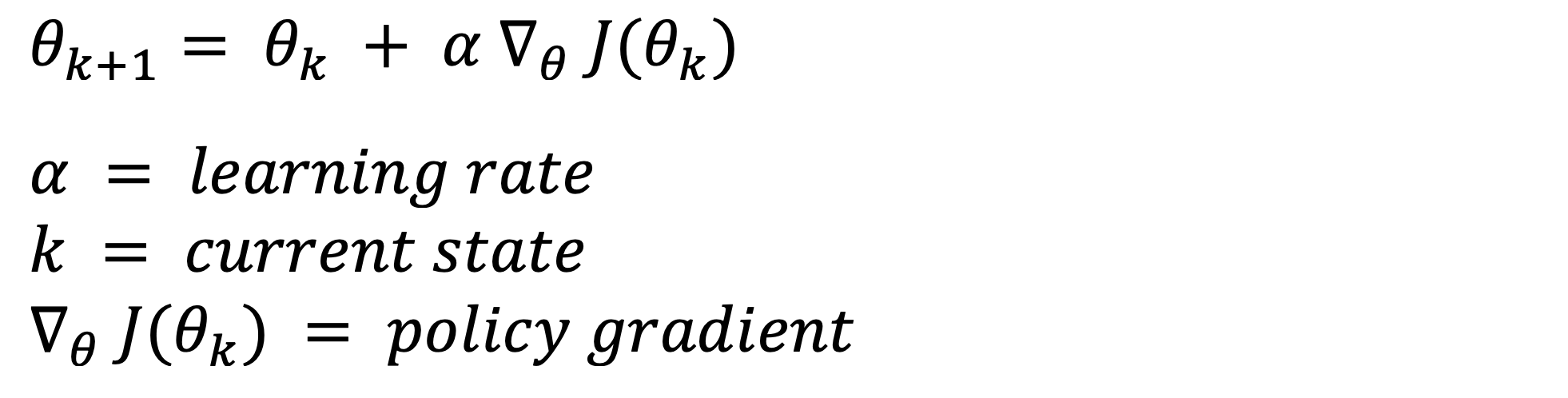
The policy gradient is the partial derivative of the objective function with respect to the policy parameters, which is used to update the parameters (model weights), and thus update the policy of the agent (our LLM). This should look very familiar to you, it's basically gradient descent, except that in gradient ascent, the sign in front of the gradient term is positive!.
But note that the reward score is not differentiable with respect to any learnable parameters because the RM simple returns a ranking score, but not the ground truth answer (since we don't have it here, like with the SFT problem). How do we calculate the policy gradient if we can't retrieve the partial derivatives of the objective function (which is a function of the reward)?
Luckily, in RL, a policy gradient can be defined in other ways, for example: In VPG, the policy gradient can defined as such (the proof for this is beyond the scope of this article, but can be found here):
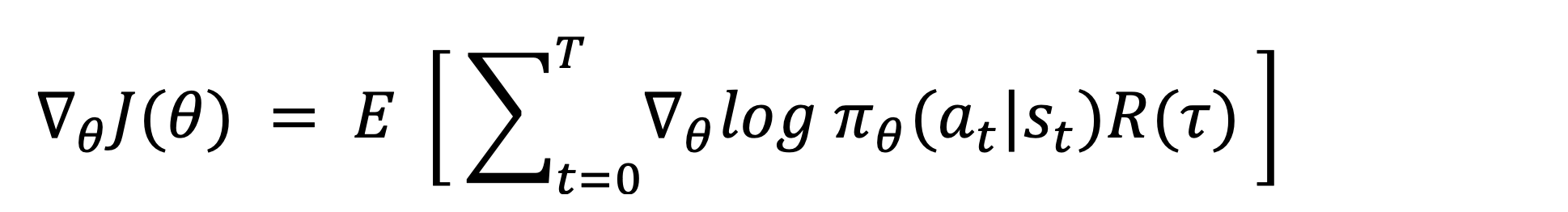
The mathematical details behind this policy gradient are irrelevant here, the point is that all policy gradient methods share the same characteristic; they update the policy parameters (LLM weights) by calculating the policy gradients and performing gradient ascent. The distinguishing feature between different policy gradient methods is how the objective function is defined, which in turn affects how we calculate the policy gradient to update our policy.
During training, policy gradients are calculated via backpropagation and used to update the model weights via a typical optimization algorithm such as stochastic gradient ascent, and this process is repeated iteratively until we have updated the model weights sufficiently. In other words, the LLMs weights are slowly adjusted such that it is incentivized to generate a response to an instruction prompt such that it maximises the objective function (which should indirectly reflect a “good” natural language response, and conversely discouraged to generate bad responses).
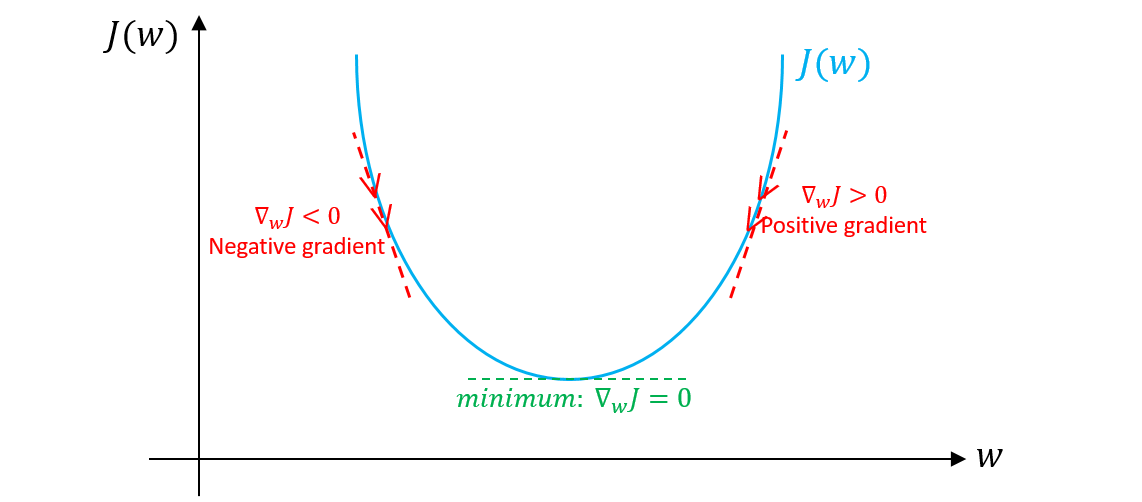
Photo credits: StackOverflow
Note: The main difference between an objective function and a loss function is that the former is used to optimize the performance (or reward received) by the LLM on a particular task, while the latter is used to measure the error of the LLMs predictions against a ground truth values during training. However, both aim to optimize their respective functions through gradient ascent/descent. Here, though I use term objective function, the subtle differences aren’t that important, and you can think of the objective function as a loss function for a RL problem.
The problems with VPG
As mentioned above, VPG is a simple algorithm, wherein the objective function is purely the reward signal for a LLM response calculated by our RM. This works fairly well in theory, but VPG suffers from several problems that can make it difficult to train our model and lead to suboptimal performance.
These problems include:
- high variance (or inconsistent policy updates) in the policy gradient estimate which can lead to slow convergence and instability during training (e.g., overshooting the global optimum),
- limited exploration, causing the model to be stuck in local optimum and fail to explore other regions to converge to the global optimum,
- limited sample efficiency, making it computationally expensive and time-consuming.
Proximal Policy Optimization (PPO)
PPO is the algorithm used by OpenAI to optimize the policy in InstructGPT, and therefore this is the one we’ll look at here. According to the PPO paper, there are two variations of PPO:
- one that makes use of the “clipped surrogate objective”, which selects the minimum of two terms, the original objective function, and a clipped version of the objective function.
- the other, which makes use of a “KL penalty coefficient”, wherein the KL (Kullback-Leiber) divergence is used to calculate the difference in two probability distributions (the updated policy and the previous policy).
In practice, both variations of PPO should ensure that the LLM generates reasonably coherent text responses. Without clipping the objective function, or the KL divergence, the optimized policy can move to a policy space that tricks the RM into giving a high reward despite generating incomprehensible text.
The PPO variation that InstructGPT adopts here is the one that makes use of the “KL penalty coefficient”, though it is not clear why they have opted for this variation when the “clipped surrogate objective” variation appears to perform better (at least for simulated robotic locomotion and Atari game playing, see paper).
I’ve placed the segment from the InstructGPT paper that defines their objective function below:

Photo credits: InstructGPT paper
The point being that with PPO, we make use of an objective function that addresses the problems of high variance, limited exploration, limited sample efficiency and inconsistent policy updates associated with VPG. Here are some ways PPO addresses these problems:
- Low variance updates: PPO uses a KL divergence penalty to ensure that the policy updates are limited, avoiding large policy changes that could lead to instability, thus making it more stable and less prone to high variance.
- Better exploration: PPO can encourage better exploration by incorporating an entropy term into the objective function. This term encourages the policy to explore a wider range of actions, instead of simply exploiting the current best action.
- Sample efficiency: PPO is designed to be more sample-efficient, as it reuses samples across multiple epochs of training. This allows it to make better use of the available training data and learn faster with fewer samples.
- Ease of implementation: at least compared to other policy gradient methods that try to address VPG’s inherent problems.
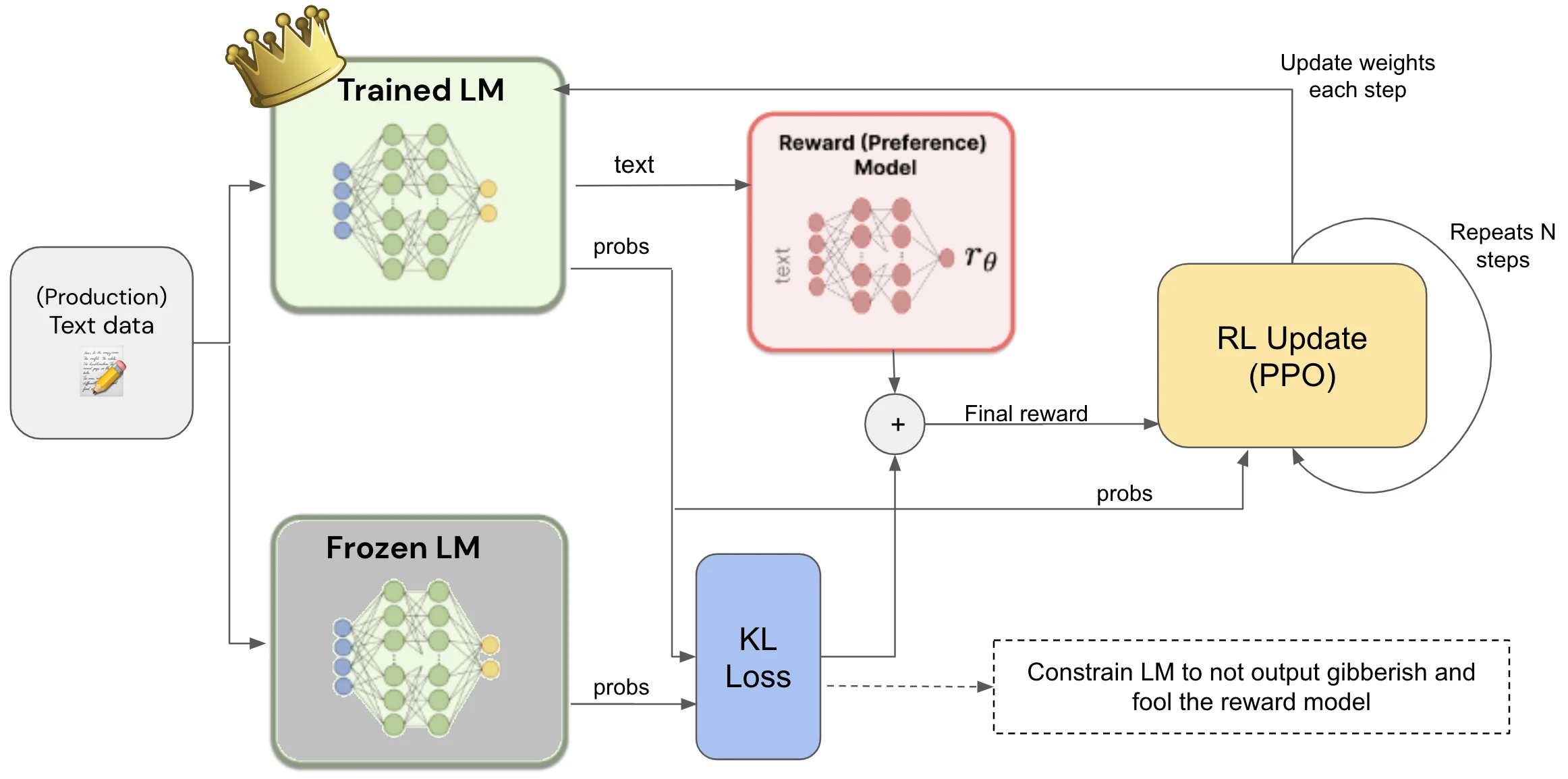
Photo credits: Reddit
Note that during RL training with PPO, we have 3 models. The frozen LLM and the LLM being trained to ensure that we can calculate the KL divergence term in the PPO objective function. And of course, the RM itself, whose weights are also frozen to ensure the ranking scores are consistent during training.
In practice, having 3 LLM models in one training environment resource heavy. For example, a full-precision 20B LLM will require 80GB GPU memory, 3 times this is 240GB (notwithstanding the training data and other considerations). There are ways to make this work in practice, such an 8-bit model instead, running on multiple GPUs (with data parallelism, model parallelism, etc.), and more. These practical considersations should not be ignored when performing such an compute intensive operation.
The advantages of RLHF
So now we can see how we can optimize a policy against the RM using PPO in RL. In step 3, a PPO dataset which includes 31k instruction prompts (no ground truth labels) are passed to the LLM to generate an output response. The LLM can then learn to update its model weights via PPO in order to optimimize the objective function (which is a function of the reward model).
But let’s consider some of the key advantages of RLHF and why this has led to such amazing results, allowing the LLM to perform well across other tasks that it has never seen before.
- RLHF removes the need for extensive ground truth labelled data (e.g. during the final RL stage, 31k instruction prompts are used here without ground truth labels, trained on 2 epochs), as the RM can provide an indicator as to how well the LLM is performing without ground truth labels (unlike regular loss functions in SFT which requires ground truth labels).
- When training the RM, we are not only encoding ranking preferences, but also encoding the ability to indirectly indicate whether the generated response actually answers the instruction prompt. Thus, our LLM is almost indirectly being trained with the SFT task, and is learning to respond to general instruction prompts, not from ground truth labels (which we don’t have) but rather from ranking preferences. Afterall, the LLM model output can’t have a high-ranking score from the RM if it doesn’t actually answer the input prompt!
- Reward scores from a RM are more flexible to the phrasing and terminology of the generated response as there is no ground truth label to specify exactly what the output should look like. Thus, providing more room and flexibility for learning and updating of model weights.
- RLHF also appears to be a suitable method for reducing bias and harmfulness in LLMs see this paper: Training a Helpful and Harmless Assistant with Reinforcement Learning from Human Feedback
Caveat: although RLHF has generated phenomenal results, work on other LLMs like Alpaca, Vicuna, etc. have shown that we can achieve close to ChatGPT-like performances without RLHF and with SFT alone. This indicates that we can think of RLHF has a method that makes up for the lack of SFT data. If we had 100k worth of perfectly curated instruction prompt data and their ground truth labels for SFT, I suspect we wouldn’t have to go through the process of RLHF and still achieve ChatGPT-like performances, or even better.
Conclusion
NLP is moving very quickly right now, and every week there are new models, papers and results that are shifting the landscape. As more research comes out, RLHF may continue to be a dominating training method for LLM, or it could also fall off to the side-lines, with a new training paradigm to replace it. Regardless of that, there is no denying that it has caused a massive shift in how we consider training LLMs and aligning them to human preferences. Understanding RLHF will only help with following the exciting research and literature coming our way.
Resources
To learn more about RL in detail:
- OpenAI's Spinning Up - Intro to DL resource
- HuggingFace's Deep RL course
- Medium post on PPO
- Medium post on RL for non-differentiable functions